Watch this week's video on YouTube
Last week we looked at how implicit conversions and datatype precedence can cause SQL Server to output unexpected results (if you aren't aware of how it handles these features).
This week I want to share another example of when SQL Server's output may surprise you: floating point errors.
Charts don't add up to 100%
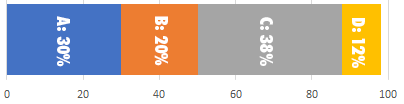
Years ago I was writing a query for a stacked bar chart in SSRS. The chart intended to show the percentage breakdown of distinct values in a table. For example, the chart would show that value A made up 30% of the rows, B made up 3%, C made up 12% and so on. Since every row had a value, I was expecting the stacked bar chart percentages to add up to 100%
However, in many instances the charts would come up short; instead of a full 100%, the percentages would only add up to 98% or 99%. What was going on?
Floats
To see an example of how this happens, let's look at the following query:
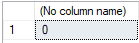
SELECT CASE WHEN CAST(.1 AS FLOAT)+CAST(.2 AS FLOAT) = CAST(.3 AS FLOAT) THEN 1 ELSE 0 END
If you've never encountered this error before, you'd expect the query to return a result of 1. However, it doesn't:
The reason this happens is that anytime you use the float datatype, SQL Server is trading off numeric precision for space savings - in actuality, that .1 in the query above is really stored as 0.10000000000000000555111512312578270212 and the .2 is stored as 0.20000000000000001110223024625156540424. Summed together, we get 0.30000000000000001665334536937734810636, not .3.
And to be clear, this isn't a problem with SQL Server - any language that implements the IEEE standard for float data types experiences these same issues.
Float Approximation
In SQL Server, the int datatype can store every whole number from -2,147,483,648 to 2,147,483,647 in only 4 bytes of space.
A single precision float, using the same 4 bytes of data, can store almost any value between between -340,000,000,000,000,000,000,000,000,000,000,000,000 and 340,000,000,000,000,000,000,000,000,000,000,000,000.
The reason floats can store such a large range is because they are only storing approximate values; some compression happens in those 4 bytes that allows SQL Server to store a wider range of data, but the increased range of values comes at the cost of losing some accuracy.
Close Enough For Horse Shoes, Hand Grenades, and Floats
In short, a float works by storing its value as a percentage within a range. As an oversimplified example, imagine representing the number 17 as 17% of the range from 1 to 100. All you need to store is the range 1,100 and the number 17%. This doesn't give us much efficiency for small numbers, but this allows us to store much larger numbers in exactly the same way. For example, to store the number 3 billion, you could make your range 1 billion (10\^9), and 10 billion (10\^10), and the percentage of 30%.
And while that oversimplified example uses base-10 to make it easy for my brain to think about, computers like doing calculations in base-2. And the math is a little bit more involved.
The Wikipedia page on floating point encoding is really good, but it uses a bunch of math notation that I haven't seen since high school. Let's reimagine that example with language we should be a little bit more familiar with: T-SQL.
A 4 byte number is made up of 32 bits. The floating point encoding breaks down these bits into 3 sections:

The first bit in blue is for the sign. This just indicates whether we will be left or right of 0 on the number line.
The next 8 bits in green indicate our exponent. This tells us which range of numbers we are in. Since we are using binary, the range is stored as a power of 2. And we only need to store the start of the range, since the end of the range would be the next power of 2.
Finally the last 23 bits in red encode the fractional location of our value within the range. Calculating our actual value then is simple as:
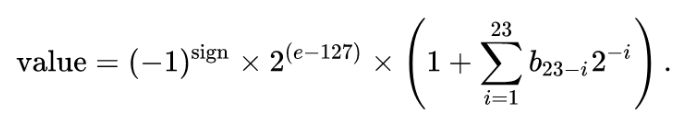
Oh yeah, I promised to do the math in T-SQL. Let's try that again.
First, we declare some variables to store the 3 encoded parts of our floating point number:
DECLARE
@sign int,
@exponent int,
@fraction decimal(38,38);
You'll notice I am storing @fraction as a decimal and not float. This is some foreshadowing about how decimal is a precise datatype that I'll come back to in a little bit.
Next we store the sign. Since we are encoding the value .15625, the sign is positive, so we set our @sign bit to 0:
SELECT @sign = 0;
Great. Now let's calculate the value of our exponent. If you've never converted binary to decimal before, you basically raise each 1 or 0 to the power of its position, so:
-- Returns 124
SELECT @exponent =
(0*POWER(2,7))
+(1*POWER(2,6))
+(1*POWER(2,5))
+(1*POWER(2,4))
+(1*POWER(2,3))
+(1*POWER(2,2))
+(0*POWER(2,1))
+(0*POWER(2,0));
Next up is converting the last 23 bits to decimal. In this case, the encoding standard specifies these are to be calculated as (1/2\^n) instead of the regular 2\^n, because we want a fraction:
-- Returns .25
SELECT @fraction =
(0*(1.0/POWER(2,1)))
+(1*(1.0/POWER(2,2)))
+(0*(1.0/POWER(2,3)))
+(0*(1.0/POWER(2,4)))
+(0*(1.0/POWER(2,5)))
+(0*(1.0/POWER(2,6)))
+(0*(1.0/POWER(2,7)))
+(0*(1.0/POWER(2,8)))
+(0*(1.0/POWER(2,9)))
+(0*(1.0/POWER(2,10)))
+(0*(1.0/POWER(2,11)))
+(0*(1.0/POWER(2,12)))
+(0*(1.0/POWER(2,13)))
+(0*(1.0/POWER(2,14)))
+(0*(1.0/POWER(2,15)))
+(0*(1.0/POWER(2,16)))
+(0*(1.0/POWER(2,17)))
+(0*(1.0/POWER(2,18)))
+(0*(1.0/POWER(2,19)))
+(0*(1.0/POWER(2,20)))
+(0*(1.0/POWER(2,21)))
+(0*(1.0/POWER(2,22)))
+(0*(1.0/POWER(2,23)));
Finally, we put them altogether like so:
-- Result: .15625
SELECT
POWER(-1,@sign)
* POWER(CAST(2 AS DECIMAL(38,37)),(@exponent-127))
* (1+@fraction)
In this example, there is no floating point error - .15625 can be accurately stored as a float. However, if go through the same exercise for a number like .1 or .2, you'll notice your numbers are not so perfect.
Fixing Floating Point Errors
Floating point math errors can be fixed in a few ways.
One option is to stop caring about them. The error occurring on floats is very small (although when compounded through arithmetic, the error can grow large enough to be noticeable like in my reporting bar chart example). If you are writing queries or reports where such a small amount of error doesn't matter, then you can continue on your merry way without having to change anything.
A second option is to still store values as floats (for that sweet, sweet storage space savings), but ensure your application code has business logic to correctly round numbers that are in precise.
However, if your data needs to be perfectly accurate every single time with no errors, use a different datatype. The logical choice here would be to use decimal in SQL Server, which uses a different internal method for storing your numbers, resulting in perfect results every time. However, the range of possible values is not as large as float, and you will pay for that precision with additional bytes of storage space.
In the end, floating point is good enough for many applications. The important thing is that you are aware that these kind of errors can happen and that you handle them appropriately.
