Watch this week's video on YouTube
Last week I needed to write a recursive common table expression. I've written them before, but it's been a while and needed to visit the documentation to reference the syntax.
Instead of going straight to the examples, I decided to read into some of the details (since skipping the details really hurt me in last week's post) and noticed this line that I had never seen before:

"Multiple...recursive members can be defined" - what????
I never knew you could have multiple recursive member statements in a CTE. Heck, I didn't even know what having multiple recursive members could do.
Since the documentation doesn't talk about them beyond the one highlighted line above, I decided to create some examples to see if I could get them to work.
FizzBuzz
FizzBuzz is a programming puzzle that asks the solver to write a program that will list the numbers 1 to 100, displaying the word "Fizz" for any numbers that are a multiple of 3, "Buzz" for any multiples of 5, and "FizzBuzz" for any multiples of 3 and 5.
I decided to try and implement the FizzBuzz problem as both a single and multiple member CTE to see how the solutions would differ.
The Basic Recursive CTE
To start out, I decided to write a CTE that lists all numbers 0 to 100:
WITH c AS
(
-- anchor member
SELECT
0 AS RowNumber
UNION ALL
-- recursive member
SELECT
c.RowNumber + 1
FROM
c /* the result of our last iteration */
WHERE
RowNumber < 100
)
SELECT *
FROM c;
The first SELECT statement in the CTE definition is known as the "anchor" member. This query runs a single time and acts as the initial result that the recursive query acts on.
The second SELECT statement in the CTE definition is known as the "recursive" member. This statement executes on the results of the previous execution (or on the results of the anchor member for the first iteration).
The recursive member will execute over and over again as long as it is still producing results. Since our recursive statement is just adding 1 to the previous result, our recursive query would run forever - which is why we add the WHERE condition stop it from executing once we reach 100.
Our final SELECT statement returns the results of our recursive CTE, providing us with a neat list of numbers from 0 to 100:

Single Recursive Member CTE for FizzBuzz
Now that our basic recursive CTE is working, let's make it solve FizzBuzz. Here is our updated code:
WITH c AS
(
SELECT
0 AS RowNumber,
'FizzBuzz' AS FizzOrBuzz
UNION ALL
SELECT
c.RowNumber + 1,
CASE
WHEN (c.RowNumber + 1) % 15 = 0 THEN 'FizzBuzz'
WHEN (c.RowNumber + 1) % 3 = 0 THEN 'Fizz'
WHEN (c.RowNumber + 1) % 5 = 0 THEN 'Buzz'
ELSE NULL
END
FROM
c
WHERE
RowNumber < 100
)
SELECT
RowNumber,
FizzOrBuzz
FROM C
ORDER BY RowNumber;
First, we add a second column to our results to display the word "Fizz", "Buzz", or "FuzzBuzz".
In the anchor member, we defaulted this value to "FizzBuzz". In our recursive member, we added a CASE statement to display the correct word. The modulo operator (%) checks to see if the current row divided by 3, 5, or 15 results in a remainder - if the remainder is 0 then we know we found a multiple of that number.
This solution is pretty easy to read and provides the expected output for our FizzBuzz puzzle:
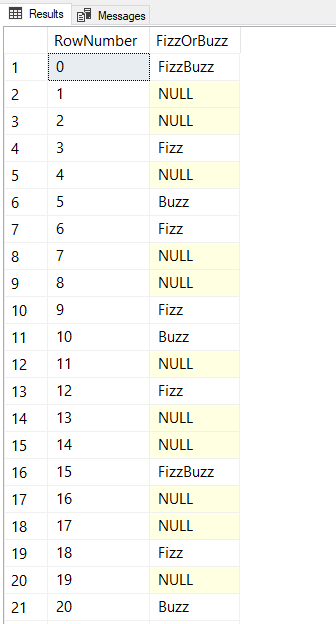
Multiple Recurisve Member CTE for FizzBuzz
Alright the moment we've been waiting for - the multiple recursive member CTE:
WITH c AS
(
SELECT
0 AS RowNumber,
'FizzBuzz' AS FizzOrBuzz
UNION ALL
/* All rows not Fizz or Buzz or FizzBuzz */
SELECT
c.RowNumber + 1,
NULL AS FizzOrBuzz
FROM
c
WHERE
c.RowNumber+1 <= 100
AND (c.RowNumber+1)%3<>0
AND (c.RowNumber+1)%5<>0
UNION ALL
/* Fizz rows */
SELECT
c.RowNumber + 3,
CAST('Fizz' AS VARCHAR(8)) AS FizzOrBuzz
FROM
c
WHERE
c.RowNumber+3 <= 100
and FizzOrBuzz in ('Fizz','FizzBuzz')
UNION ALL
/* Buzz rows */
SELECT
c.RowNumber + 5,
'Buzz' AS FizzOrBuzz
FROM
c
WHERE
c.RowNumber+5 <= 100
and FizzOrBuzz in ('Buzz','FizzBuzz')
)
SELECT
RowNumber,
STRING_AGG(FizzOrBuzz,'') AS FizzOrBuzz
FROM C
GROUP BY
RowNumber
ORDER BY RowNumber
You'll notice we have 3 recursive members: the first generates all rows up to 100 that are not multiples of 3 or 5, the second generates all rows that are multiples of 3, and the third statement generates all rows that are multiple of 5.
If we were to run SELECT \* FROM c; after only making the mentioned changes, you'll notice that it looks like things are mostly working, but that we have duplicates (and incorrect labeling) for rows that are multiples of 3 and 5:
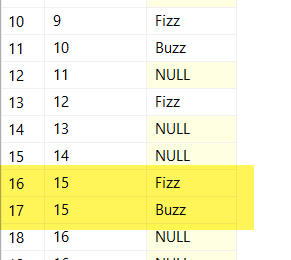
The way I decided to fix that is by adding a STRING_AGG() function to the final SELECT statement, concatenating the outputs of rows with the same RowNumber. With that addition, our multiple recursive member CTE FizzBuzz solution is complete.
One thing to be aware of in the above solution: each of the recursive member statements will execute on the previous results of ANY recursive member statement, so we add the conditions "...and FizzOrBuzz in ..." to force each recursive statement to run only on the output from its own previous result. This feels like cheating a little bit, but it was the only way I could solve the problem I had defined.
Practical Examples and Further Reading
I had a hard time coming up with a practical uses for multiple recursive member CTEs.
I searched online for some examples but it doesn't seem like many people have written about the topic. One exception I did find was an article by Itzik Ben-Gan where he uses them to solve Lord of the Rings family trees (heh).
Honestly though, as excited as I was initially to learn that doing this is possible, I don't know if/when I'll ever use it. I'm hoping I encounter a problem one day that can make use of multiple recursive statements, but who knows if that will ever happen.
If you have used multiple recursive member CTEs to solve a real-world problem before, leave me a comment - I'd love to hear about the scenario you used it in.
